
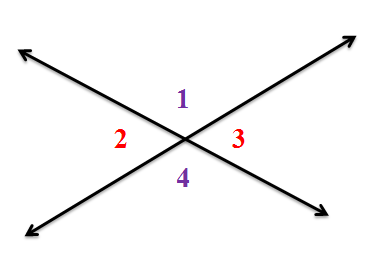
You can use that awareness to solve seemingly difficult algebraic problems like this:ĭraw parallel lines MJ and TE and the transversal AS with intersecting Point C on Line MJ and intersecting Point I on Line TE, spelling in a circular way MAJESTIC. Once you understand the relationship between the two angles, you can assume some basic facts, such as their congruence or that they may be supplementary. Whether the two angles under investigation are on the same side of the transversal (consecutive) or opposite sides of the transversal (alternate) Whether the angles are outside the parallel lines (exterior) or inside the parallel lines (interior) Relative positions of the two questioned angles When viewing any new figure, go through your list and determine three things: You can use your newfound knowledge of angle relationships to solve algebraic challenges about geometric figures. And, of course, ∠RYL pairs off as the alternate interior angle of ∠TLY. In our figure, ∠ALY is the alternate interior angle for ∠YLO, making them congruent. They lend themselves to the Alternate Interior Angles Theorem, which states that congruent alternate interior angles prove parallel lines (much as the Alternate Exterior Angles Theorem did). Also d and e are a pair of Alternate Interior Angles. In this example c and f are a pair of Alternate Interior Angles. When the interior angles are on opposite sides of the transversal, they are alternate interior angles. When two lines are crossed by another line (called the Transversal ): Alternate Interior Angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. In parallel lines, consecutive interior angles are supplementary. The only other pair of consecutive exterior angles is ∠DYR and ∠OLI.Īngle relationships - consecutive interior angles

In our figure above, ∠AYD and ∠TLI are consecutive exterior angles. When the exterior angles are on the same side of the transversal, they are consecutive exterior angles, and they are supplementary (adding to 180°). You can see two types of exterior angle relationships: Consecutive exterior angles An exterior angle among line constructions (not polygons) is one that lies outside the parallel lines. Those same parallel lines and their transversal create exterior angles.
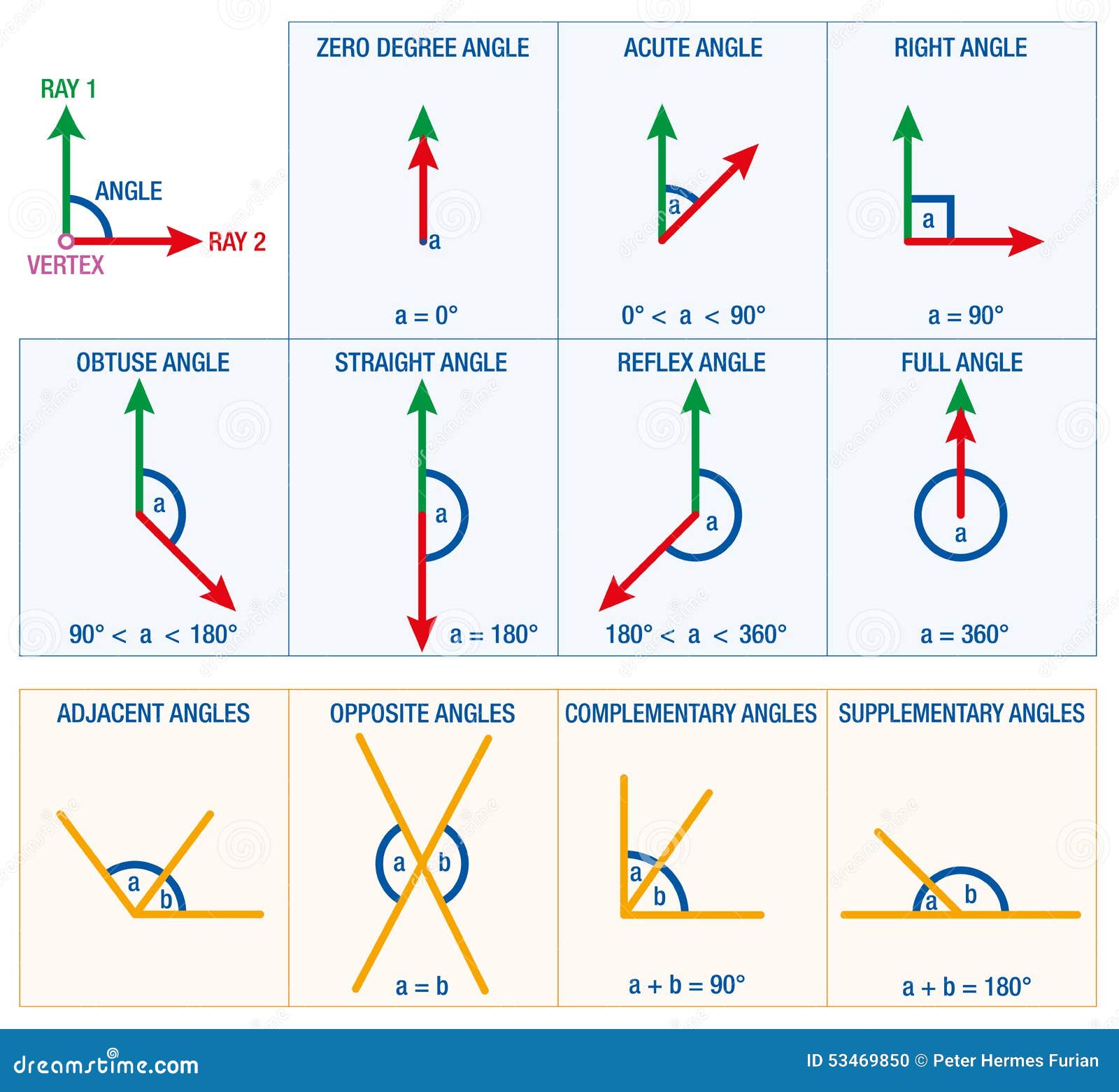
In all cases, since our Line AR and TO are parallel, their corresponding angles are congruent. You found ∠RYL corresponding to ∠OLI, right?Īnd you did not overlook ∠AYL corresponding to ∠TLI, did you? Our transversal and parallel lines create four pairs of corresponding angles. When the corresponding angles are on parallel lines, they are congruent. Angles that have the same position relative to one another in the two sets of four angles (four at the top, Line AR four at the bottom, Line TO) are corresponding angles. We can adroitly pull from this figure angles that look like each other. Angle relationships - corresponding angles


 0 kommentar(er)
0 kommentar(er)
